Interpolation

Unter Interpolation versteht man z.B. im Bereich der Computergrafik, in welcher Art Werte zwischen Keyframes berechnet werden. Mathematisch betrachtet liegen diskrete Werte vor, zu denen eine stetige Funktion gefunden werden soll.

Zeitliche Interpolation

Keyframe-Interpolation

Die zeitliche Interpolation hat Einfluss auf die Geschwindigkeit, mit der ein Parameter geändert wird. Gängige Möglichkeiten sind:

• Constant (rot)
  Der Parameterwert ändert sich beim Erreichen eines Keyframes sprunghaft auf den neuen Wert. Die Keyframes sind in der grafischen Darstellung durch eine Stufe verbunden.
  Constant Keyframes finden meist Anwendung, wenn ein Parameterwert umgeschaltet werden soll.
• Linear (pink)
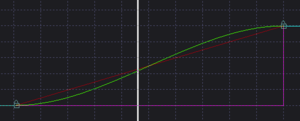
  Der Parameterwert ändert sich mit konstanter Geschwindigkeit. Die Keyframes sind in der grafischen Darstellung durch eine gerade Linie verbunden.
  Die Parameteränderung beginnt/endet abrupt. Diese Interpolation findet z. B. Anwendung beim erstellen von gleichmäßig durchlaufenden Änderungen in Loops.
• Bezier (grün)
  Der Parameterwert ändert sich mit veränderlicher Geschwindigkeit. Diese nimmt anfangs zu und beim erreichen des folgenden Keyframes wieder ab. Die Keyframes sind in der grafischen Darstellung durch eine S-förmige Kurve verbunden.
  Die Parameteränderung beginnt/endet langsam, was natürlichen Prozessen entspricht. Eine Anwendung in Loops verursacht immer eine Pause am Loop-Punkt.

Räumliche Interpolation

räumliche Interpolation

Die räumliche Interpolation findet man bei animierten Bewegungen im Raum. Sie legt fest, welchen Weg ein Objekt zwischen zwei Positionen zurücklegt. Gängige Möglichkeiten sind:

• Linear
  Hierbei erfolgt der Ortswechsel geradlinig zwischen Start und Zielpunkt. (Punkte 3 und 4)
• Bezier
  Der Ortswechsel erfolgt auf einer geschwungenen Bahn, die meist einen Bezierpfad zur Grundlage hat. (Punkte 1 und 2)

Beide Interpolationsarten sind voneinander unabhängig. So kann sich ein Objekt mit konstanter Geschwindigkeit auf einer Kurve von A nach B bewegen. Genauso ist es möglich, dass ein geradliniger Weg mit veränderlicher Geschwindigkeit zurück gelegt wird.